3. Time-Entropy Mapping|Computable Multiplicative Entropy
3 Definition and analysis formula of entropy In this definition of entropy, the entropy value of a closed system at a given moment (i.e., during a specific state transition) is calculated as the multiplicative product of the energy norms of all SEQ involved in that transition(that moment's space transformation)
.Entropy value of closed system S=∏mᵢ, i∈N ①
Energy of closed system=constant=∑mᵢ, i∈N ②
Sₘₐₓ≤mᵢⁿ , When all mᵢ are equal or differ only by Planck's constant h.
(Where mᵢ refers to the energy carried by the ith SEQ during a single transformation of the closed system, where each energy state mᵢ is an integer multiple of Planck’s constant h, mᵢ=nᵢh, nᵢ∈N)
3.1 Energy transfer rules and triggering conditions:
Energy exchange occurs between adjacent SEQ (i,j) if and only if the following thermodynamic gradient exists: mᵢ>mⱼ+h, Energy transfer occurs only in discrete quanta of Planck's constant h, mᵢ→ mᵢ−h; mⱼ→mⱼ+h (Planck's constant:h)3.2 Numerical Example: System States and Entropy Evolution
Table.1: Simplified Entropy Increase Demonstration
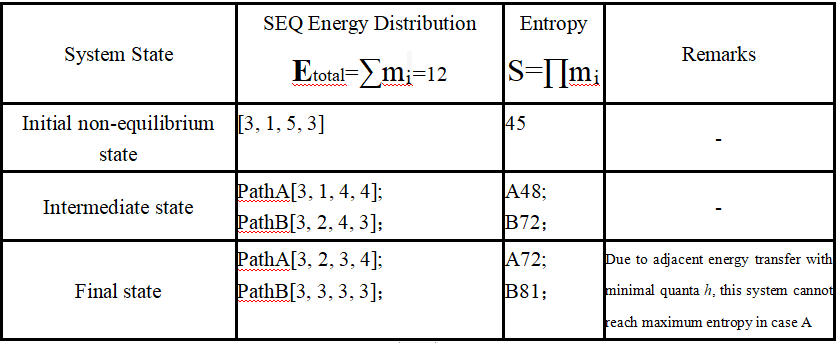
Note:The above analysis demonstrates that different entropy-increasing pathways exhibit distinct sequences of entropy variation.
3.3 Logarithmic Relation:
After logarithmic transformation, lnS aligns with the conventional Boltzmann entropy form, while the multiplicative formulation naturally suits discrete systems.
3.4 Proof of Spontaneous Entropy Increase
Spontaneity Theorem of entropy increase (Second Law of Thermodynamics):
For every possible energy transfer process, the total entropy change satisfies ΔS≥0.
Proof Outline: Let the pre-transfer states be mᵢ=a, mⱼ=b (a>b+h);
The post-transfer entropy ratio is:
Sₜ₁/Sₜ₂=(a−h)(b+h)/ab=1+h(a−b−h)/ab>1 (Planck's constant h)
3.5 Entropy increase manifests through macroscopic interactions level, atomic/molecular level, QED processes, and microscopic particle restructuring (matrix disintegration/reorganization, radiation).
3.6 The entropy formulation S=∏mᵢ, i∈N proposed herein operates not only at the fundamental SEQ level, but also admits coarse-graining for arbitrary massive many-body systems. This universality originates from the energy-mass equivalence which allows the cumulative product to naturally encode multi-body interactions. Crucially, this formulation provides first-principles computational constraints for discrete simulations across all scales.
3.7 The definition conserves energy, has an entropy ceiling, ensures spontaneous increase, and logarithmically aligns with classical entropy.
Indeed, this model establishes a novel analytic quantum thermodynamic framework where coarse-graining automatically enforces the indistinguishability of microscopic particles in physical properties while simultaneously characterizing the entropy-increasing process of energy homogenization. These properties collectively confirm the validity of this entropy definition.
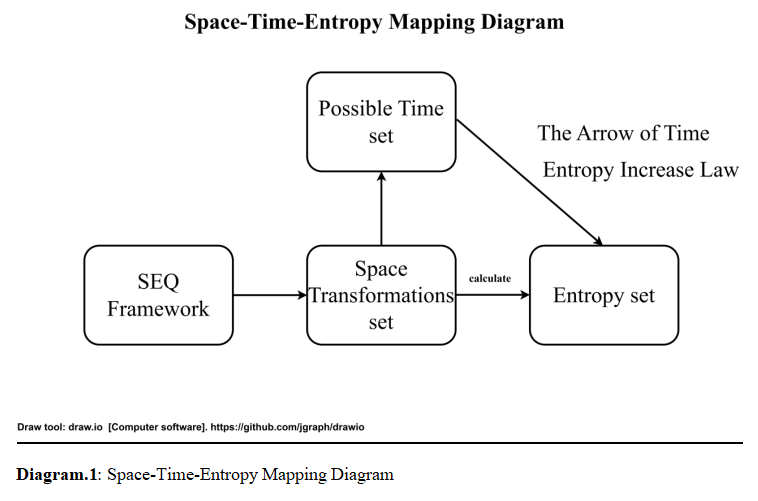
At this point, a clear multiple mapping can be established:
One space transformation→one entropy value→One possible moment
3.8 The Spontaneous Entropy Increase is Causality.
The existence of isoentropic transformations implies that even with the constraint of the least action principle further limiting the degrees of freedom in future spatial transformation paths, the potential spacetime evolution trajectories are not necessarily unique. Within this model's framework, multiple solutions may satisfy the least action condition, indicating that while causality adheres to Markovian properties, a certain dynamic freedom persists.
The existence of isoentropic transformations and different entropy-increasing pathways imply that even with the constraint of the least action principle further limiting the degrees of freedom in future spatial transformation paths, the potential spacetime evolution trajectories are not necessarily unique. Within this model's framework, multiple solutions may satisfy the least action condition, indicating that while causality adheres to Markovian properties, with a certain dynamic freedom persists.
3.9 Why Analytic Entropy is Adopted: Within this model's framework, physical states at Planck-time scales exhibit deterministic characteristics. Although current experimental conditions cannot directly measure them, traditional statistical entropy can be reduced to analytic expressions at this scale. This perspective not only reveals the microscopic essence of statistical quantities but also provides a new analytic foundation for quantum thermodynamics—unifying macroscopic statistical behaviors with deterministic dynamics at the Planck scale.

